
There is another story about Euclid in which a student wanted to know what he was going to get for learning geometry. Euclid answered, "There is no royal road to geometry" and sent the young King off to study. One day, the King asked Euclid if there was an easier way for him to learn geometry than by studying. The young King of Egypt was once one of his students. Very little is known about Euclid's personal life, but he did start a school in Alexandria and worked hard to help his students learn. Though much of his time was invested in the workings of light, Euclid is most known for his mathematical presence, specifically in geometry. The ancient Greek scientist and mathematician Euclid, who lived 2300 years ago in Alexandria, Egypt, was one of the first to explain how light reflects off of a mirror. Historical Vignette: Euclid and His Students Put them together in small groups so they can try playing the games they designed. Have them write instructions and develop diagrams to help explain their games. Encourage them to make up a game in which they use flashlights to reflect light off of a mirror onto a goal or target. Then have them think about how a basketball bounces off the backboard of a basketball goal. Game - Discuss with students how light reflects off a mirror like a ball bounces off a surface.

Now write a short story about your magical mirror. Use your imagination and think about how mirrors could be used in magical ways. Writing - Use the following as a narrative writing prompt: In the fairy tale Sleeping Beauty and in the story Through the Looking Glass, mirrors are magical. Discuss ahead of time how mirrors are used in both stories and how the use of mirrors allows characters to see and do things they could not do in a real world. Reading - Either read aloud or have students read the fairy tale Sleeping Beauty or the book Through the Looking Glass before they go onto the narrative writing prompt. Each team of students should be able to explain to another group how they constructed the protractors and how they used the tools to measure the angles. Ask them to draw and record their results in their science notebooks. Then, have students design and construct large protractors out of cardboard to measure their angles of incidence and reflection.
#Angle of reflection equals angle of incidence how to#
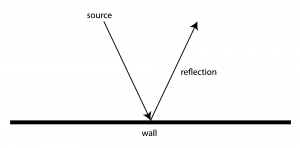
Mathematics - Show students how to use protractors to measure angles. Pairs of students will continue doing this until they have found and marked the places where they must stand to see both reflections in the mirror.Īngles of Reflection Explore how light reflects off of a mirror at different angles. Once students have determined where they will stand, they remove the paper from the mirror and test their predictions. They will draw diagrams in their science notebooks to show the places they have selected. Each pair will discuss and agree on the places where they think they must stand. They will be challenged to predict where two people must stand so each can see the other's reflection in the mirror. Students will then work in pairs using the student page as a guide. Making sure to use the mirror as a centerline, have students lay a 2 to 3 meters length of masking tape on the floor, extending out from, and perpendicular to, the wall. Students will mount the mirror, which should be covered with a piece of paper, flat on a wall at eye level. In other words, when light comes into contact with a mirror, the angle of reflection equals the angle of incidence. According to the law of reflection, light is always reflected at the same angle that it arrives at a surface. The angle between the reflected ray and the perpendicular is called the angle of reflection. The angle between the incident ray and an imaginary perpendicular line drawn to the surface of the mirror is called the angle of incidence. Reflection involves two types of light rays: the incoming, or incident, ray and the outgoing, or reflected, ray. When you look at an object in a mirror, what you see is the reflection of light from that object. Mirror, Mirror on the Wall: Angles of Reflection Molecular Expressions: Science, Optics and You - Activities in Optics - Angles of Reflection


 0 kommentar(er)
0 kommentar(er)
